四轴飞行器完全指南0x01 - Arduino、姿态解算和滤波

说来这个“好想做个四轴飞行器玩啊”的想法不知不觉就已经一个年头了呢，谁能想到当年这么随便的一个脑洞如今变成了学校的科研项目OTZ 既然拿了人家的经费，也就没有不把它做出来的道理，于是就这样愉快地把过程记录下来吧！

#目录

那么，开始制作吧！

#有关Arduino的两三事

##前期准备

在这里先解释一下：目前流行的四轴飞行器有两种形式，即有刷四轴和无刷四轴。这里的“刷”指的就是四轴所用的电机里的碳刷，起到了换向器的作用。具体的原理请参见这里。虽然无刷电动机在控速、稳定性、重量上均优于有刷电机，但是由于其结构复杂，难（cheng）度（ben）高等原因，我们这里采用的还是有刷电机。只不过，我们用到的是名为“有刷空心杯电机“的神器！体积小，重量轻，能量密度大，你值得拥有（雾）。

要制作一块开发版，你需要：

1
2
3
4
5
6
7
8
9
10
1. 面包板 				x 1
2. 杜邦线 				x 40p
3. Arduino mini Pro 3.3v 		x 2
（当然uno更好，还省去了USB的麻烦。此外一定要根据所选模块的支持电压选购Arduino，不要像吾一样买了5v还得上变压器）
4. MPU6050模块（GY—85）			x 1
（这个是六轴传感器模块，资料最丰富）
5. nrf24l01模块 				x 1
（2.4GHz通讯模块，可依个人喜好更改）
6. USBtoUART转接器 			x 1
（买UNO的可以忽略这条了，mini没有USB接口）

以上。

##I2C总线

有了这些材料，如何把它们连接起来呢？当然用杜邦线！（废话）但是这只是宏观的表象，这些电子元件之间是通过I2C总线相连接的。I2C总线只有两条，其中一条是数据线（SDA），一条是时钟线（SCL）。I2C总线采用7比特长度的地址空间来寻找设备，所以我们的设备地址会被表示为类似于0x53这样的十六进制数字。在这里，我们采用的是主从模式，即Arduino（master）-> 多个模块（slave）
可以在现在将MPU6050模块与Arduino连接。

###I2C总线的连接方法

1
2
3
4
5
6
7
modules                             Arduino
--------------------------------------------
VCC_in(5v)
3.3v                ------>        VCC
GND                 ------>        GND
SCL                 ------>        A5(SCL)
SDA                 ------>        A4(SDA)

###Arduino中的I2C库

Arduino中已经预先定义了I2C相关的库，只需要简单的导入Wire.h就能使用其中的函数了。
可以参见这里了解更多。

##UART总线

##MPU6050模块

#有关算法

##什么是姿态解算？

姿态解算，简而言之就是根据四轴上传感器读取的数据来计算当前时刻四轴的姿态，即获取四轴的Roll（X轴旋转角度）、Pitch（Y轴旋转角度）、Yaw（Z轴旋转角度）。这张图可以直观的解释：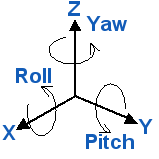
Roll、Pitch、Yaw
根据习惯，我们一般将Z轴定义为重力加速度参考方向，垂直于地面。因此，Roll和Pitch就表示飞行器是否平稳，Yaw则表示水平飞行的方向。这样一来，我们就有了表示四轴姿态的参考系。

现在让我们想像一下让整个坐标系绕X轴旋转了alpha度，即YZ构成的平面绕X轴旋转了alpha度。这时我们发现，只需用一个arctan函数就可以求出alpha。以代码的形式表示就是

1
alpha = atan2(acc_y, acc_z)

这里的atan2函数是arctan的变体，atan2（x, y)表示arctan(y/x)，acc_y, acc_z表示加速度计在Y、Z轴的读数，也就是地心引力的分量。
同理，我们可以得到：

1
2
Roll  = atan2(acc_y, acc_z)
Pitch = atan2(acc_z, acc_x)

让我们忍住写下Yaw = atan2(acc_x, acc_y)的冲动。

你一定发现了，由于我们把Z轴设置成了参考方向，它的方向是与重力加速度方向平行的。换句话说，当我们在旋转Z轴的时候，理想状况下，加速度计给我们的数值永远会是(0, 0, 1)。这样我们将不能计算出飞行器的偏航。Sad story。

那么我们是不是没有办法了呢？且看下回分晓（误

##加一点滤波！
俗话说的好，“兼听则明”。这么重要的飞行大业，也不能单单只听一个小小的加速度计说了算不是。更何况加速度计这家伙非常的不靠谱，在运动过程中给出多少个G的加速度都有可能。所以现在我们请来陀螺仪这个同样不靠谱的家伙来协助我们测量(喂)。

前面说到了加速度计在运动过程中不靠谱，实际上陀螺仪呢，会随着时间的推移越来越不靠谱。也就是所谓的“积分误差”是也。

积分误差在短时间内并不是什么大问题，但是经过几秒的累计后，就有可能累积到非常大的数值。于是聪明的前辈就想到了同时利用加速度计和陀螺仪二者的数据，融合二者的数据来解算姿态。用代码写出来是这样:

1
2
#融合一个轴的数据
angle = (acc * w1 + gyro * w2) / (w1 + w2)

其中w1，w2是参数。这个式子也可以化简为下面这样:

1
2
#化简后
angle = (acc + gyro * wGyro) / (1 + wGyro)

说白了其实就是加权平均数的思想，其中的wGyro参数就表示了对两个传感器的信任程度。这个参数的取值是个非常烦人的事儿，请根据个人喜好慢慢调试吧w （这里采用的是2.5，目前感觉不错）

根据上面的式子就很容易写出所有的表达式了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
//完整的c代码示例，有空再回来优化了otz
#ifndef __Filter__
#define __Filter__

#include <math.h>

#define pi (180 / 3.1415)

const float wGyro = 2.5;
const float dt    = 0.004;

static float angle[3];

void angle_init(float acc[3])
{
truefloat R_acc = sqrt(acc[0] * acc[0] + acc[1] * acc[1] + acc[2] * acc[2]);

trueacc[0]  /=  R_acc;
trueacc[1]  /=  R_acc;
trueacc[2]  /=  R_acc;

trueangle[0] = atan2(acc[1],acc[2]) * pi;
trueangle[1] = atan2(acc[0],acc[2]) * pi;
trueangle[2] = atan2(acc[0],acc[1]) * pi;
}


void filter(float acc[3], float gyro[3], float mag[3])
{
truefloat R_acc = sqrt(acc[0] * acc[0] + acc[1] * acc[1] + acc[2] * acc[2]);

trueacc[0]  /=  R_acc;
trueacc[1]  /=  R_acc;
trueacc[2]  /=  R_acc;
true
trueangle[0] = (atan2(acc[1], acc[2]) * pi  +  (angle[0] + gyro[0] * dt) * wGyro) / (1 + wGyro);
trueangle[1] = (atan2(acc[0], acc[2]) * pi  +  (angle[1] + gyro[1] * dt) * wGyro) / (1 + wGyro);
trueangle[2] =           mag[2]             +  (angle[2] + gyro[2] * dt) * wGyro) / (1 + wGyro);
}

#endif

就是这样了！好的程序员是从来不写注释的！（<-其实只是单纯的懒而已）什么时候有空了再回来搞三个传感器的融合吧。

###其他的方法
在这里暂且只说到了这样超～级简单的互补滤波算法，某种意义上这也是工业派的胜利吧（笑。要说我这个不折不扣的学院派为什么会选择这样的算法来用的话呢……当然是因为它足够简单啊！才不是什么我学不会呢！
好吧。我就是没学会。目前还有两种更高级的办法来滤波:

  • 卡尔曼滤波
  • 梯度下降法滤波

这个坑填完了可能会试着去研究一下吧。不过卡尔曼的精髓也无非就是动态调参数罢了，没什么了不起哼！

以上，差不多就是当前的进度了。下一节的内容是PID和电机控制，才……才不期待你们看呢哼！